构建乘积数组

题目：

​ 给定一个数组 A[0,1,...,n-1]，请构建一个数组 B[0,1,...,n-1]，其中B中的元素 B[i]=A[0]A[1]...*A[i-1]A[i+1]...*A[n-1]。不能使用除法。

分析：

例如：A[]={1,2,3} 求 B[]

B[0]=A[1]×A[2]=2×3=6

B[1]=A[0]×A[2]=1×3=3

B[2]=A[0]×A[1]=1×2=2

1. B[0]初始化为1，从下标 i=1开始，先求出 C[i] 的值并放入B[i],即B[i]=C[i]=C[i-1]×A[i-1]，所以B[1]=B[1-1]×A[1-1]=B[0]×A[0]=1×1=1，i++
2. B[2]=B[2-1]×A[2-1]=B[1]×A[1]=1×2=2，i++超出长度停止循环
3. C[i]计算完毕求D[i]，设置一个临时变量temp初始化为1
4. 从后往前变量数组，LengthA=3初始化i=LengthA-2=1,结束条件为i>=0
5. 第一次循环，temp=temp×A[i+1]=1×A[2]=3,计算出A中最后一个元素的值放入temp,temp相当于D[i]的值
6. 因为之前的B[i]=C[i],所以让B[i]×D[i]就是要保存的结果，即B[i]=B[1]=B[1]×temp=1×3=3,i–=0
7. 计算B[i]=B[0],temp上一步中的值是A[2],在这次循环中temp=temp×A[0+1]=A[2]×A[1]=3×2=6
8. B[i]=B[0]=B0]×temp=1×6=6,i–<0循环结束

所以B数组为{6,3,2}

代码：

class MultiplySolution {

    /**
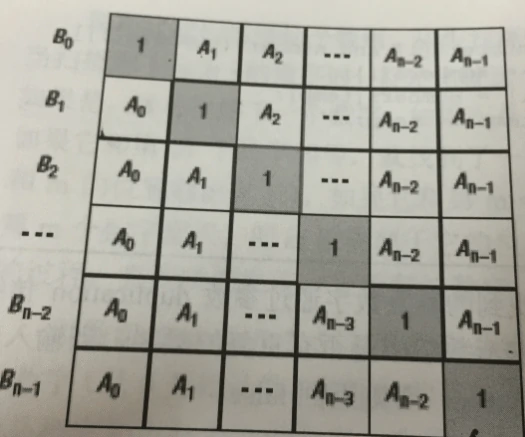
     * 这道题的中心思想是将返回的数据列成一个矩阵，每一个矩阵的行向量都是一个从a(0)到a(n-1)
     *   ,然后这个对角线都是1.那么此时B0的值就是A0为一，剩下的行向量相乘
     * @param data
     * @return
     */
    public static int[] multiply(int[] data) {
        int length = data.length;
        int[] param = new int[length];
        param[0] = 1;

        for (int i = 1; i < length; i++) {
            param[i] = param[i - 1] * data[i - 1];
        }

        int temp = 1;
        for (int i = length - 2; i >= 0; i--) {
            temp *= data[i + 1];
            // temp始终会记录值，每次只需要加上这行上三角没有乘进来的数就可以了。
            param[i] *= temp;
        }

        return param;
    }

    public static void main(String[] args) {
        int[] data = {1, 2, 3};
        System.out.println(Arrays.toString(multiply(data)));
    }
}

参考：

https://blog.csdn.net/qq_28081081/article/details/80875917

https://blog.csdn.net/gatieme/article/details/51541100