树的子结构

题目：

​ 输入两课二叉树A和B，判断B是不是A的子结构。二叉树节点的定义如下：

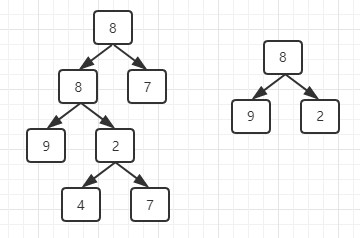
public class BinaryTreeNode {
    public int value;
    public BinaryTreeNode left;
    public BinaryTreeNode right;
}

如下图中，二叉树B即为A的子结构

分析：

先判断两棵二叉树的根节点是否相等：

1. 相等

分别判断两棵二叉树左子节点，右子节点是否相等：

1. 相等：分别判断左子节点的左、右子节点和右子节点的左、右子节点是否相等，一直到整棵树遍历完成；

2. 不相等：当前节点不存在子结构。

3. 不相等

   判断左子树中是否包含子结构。

   判断右子树中是否包含子结构。

代码：

public class CheckSubTree {

    /**
     * 判断是否存在子树
     * @param pRoot1 二叉树1根节点
     * @param pRoot2 二叉树2根节点
     * @return boolean
     */
    public static boolean hasSubTree(BinaryTreeNode pRoot1, BinaryTreeNode pRoot2) {

        boolean result = false;

        // 两棵二叉树都不为空
        if (null != pRoot1 && null != pRoot2) {

            // 判断当前节点是否相等
            if (isEqual(pRoot1, pRoot2)) {
                // 判断是否存在包含关系
                result = contains(pRoot1, pRoot2);
            }

            // 如果不相等，判断左子树
            if (!result) {
                result = hasSubTree(pRoot1.left, pRoot2);
            }

            // 如果不相等，判断右子树
            if (!result) {
                result = hasSubTree(pRoot1.right, pRoot2);
            }
        }

        return result;
    }

    /**
     * 判断前者是否包含后者
     * @param pRoot1 前者根节点
     * @param pRoot2 后者根节点
     * @return boolean
     */
    private static boolean contains(BinaryTreeNode pRoot1, BinaryTreeNode pRoot2) {

        // 如果后者为空，返回true
        if (pRoot2 == null) {
            return true;
        }

        // 如果后者不为空，前者为空，返回false
        if (pRoot1 == null) {
            return false;
        }

        // 判断根节点是否相等，如果不相等，则不包含
        if (!isEqual(pRoot1, pRoot2)) {
            return false;
        }

        // 分别判断左节点和右节点是否都相等
        return contains(pRoot1.left, pRoot2.left) && contains(pRoot1.right, pRoot2.right);
    }

    private static boolean isEqual(BinaryTreeNode node1, BinaryTreeNode node2) {

        if (null == node1 || null == node2) {
            return false;
        }

        return Integer.valueOf(node1.value).equals(node2.value);
    }
}

测试：

public class CheckSubTreeTest {

    BinaryTreeNode root1 = new BinaryTreeNode(8);
    BinaryTreeNode root2 = new BinaryTreeNode(8);

    @Before
    public void before() {

        BinaryTreeNode nodeA11 = new BinaryTreeNode(8);
        BinaryTreeNode nodeA12 = new BinaryTreeNode(7);
        BinaryTreeNode nodeA21 = new BinaryTreeNode(9);
        BinaryTreeNode nodeA22 = new BinaryTreeNode(2);
        BinaryTreeNode nodeA31 = new BinaryTreeNode(4);
        BinaryTreeNode nodeA32 = new BinaryTreeNode(7);

        BinaryTreeNode nodeB11 = new BinaryTreeNode(9);
        BinaryTreeNode nodeB12 = new BinaryTreeNode(2);

        buildTree(root1, nodeA11, nodeA12);
        buildTree(nodeA11, nodeA21, nodeA22);
        buildTree(nodeA22, nodeA31, nodeA32);

        buildTree(root2, nodeB11, nodeB12);
    }

    @Test
    public void test() {

        boolean hasSubTree = CheckSubTree.hasSubTree(root1, root2);
        System.out.println(hasSubTree);
    }

    private void buildTree(BinaryTreeNode root, BinaryTreeNode left, 
                           BinaryTreeNode right) {
        root.left = left;
        root.right =right;
    }
}