二叉搜索树与双向链表

题目：

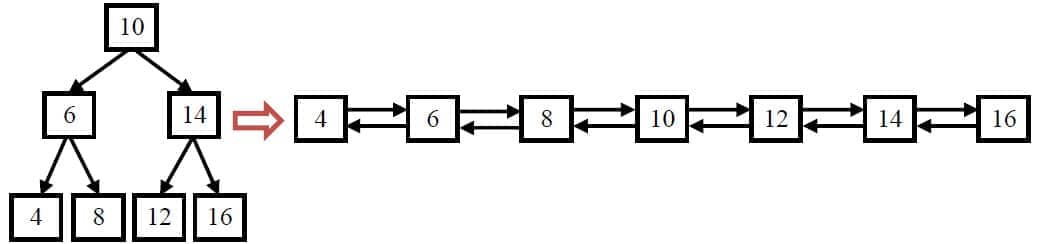
​ 输入入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。比如输入下图中左边的二叉搜索树，则输出转换之后的排序双向链表。

二叉树节点的定义如下：

public class BinaryTreeNode {

    public int value;
    public BinaryTreeNode left;
    public BinaryTreeNode right;
}

分析：

​ 在二叉树中，每个节点都有两个指向子节点的指针。在双向链表中，每个节点也有两个指针，分别指向前一个节点和后一个节点。这两种结构相似。在搜索二叉树中，左节点的值总是小于根节点，右节点的值总是大于根节点，因此再将二叉搜索树转成双向链表的过程中，原先指向左节点的指针调整为指向前一个节点，原先指向右节点的指针调整为指向后一个一个结点。

​ 由于要求转换之后的链表是排好序的，我们可以使用中序遍历来遍历二叉树，因为中序遍历是按照从小到大的顺序遍历每个节点。当遍历到根节点的时候，我们把树看成 3 部分：值为10的节点，根节点为 6 的左子树，根节点为 14 的右子树。

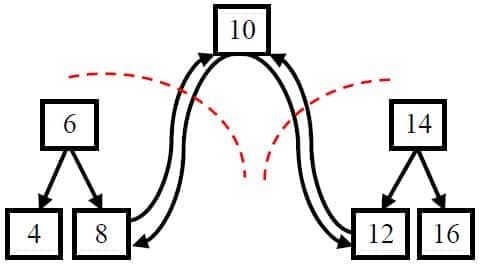
​ 最后，按照中序遍历的顺序，当我们遍历转换到根结点（值为10的结点）时，它的左子树已经转换成一个排序的链表了，并且处在链表中的最后一个结点是当前值最大的结点。我们把值为8的结点和根结点链接起来，此时链表中的最后一个结点就是10了。接着我们去遍历转换右子树，并把根结点和右子树中最小的结点链接起来。

​ 很明显，转换它的左子树和右子树，由于遍历和转换过程是一样的，很自然地想到可以用递归。

代码：

public class ConvertBinaryTreeToLinkedList {

    public static BinaryTreeNode convert(BinaryTreeNode pRoot) {
        BinaryTreeNode lastNode = null;
        convertNode(pRoot, lastNode);
        BinaryTreeNode headOfList = lastNode;
        while (headOfList != null && headOfList.left != null) {
            headOfList = headOfList.left;
        }
        return headOfList;
    }

    private static void convertNode(BinaryTreeNode pNode, BinaryTreeNode lastNodeInList) {
        if (pNode == null) {
            return;
        }

        BinaryTreeNode currentNode = pNode;
        if (currentNode.left != null) {
            convertNode(currentNode.left, lastNodeInList);
        }

        currentNode.left = lastNodeInList;

        if (lastNodeInList != null) {
            lastNodeInList.right = currentNode;
        }

        lastNodeInList = currentNode;

        if (currentNode.right != null) {
            convertNode(currentNode.right, lastNodeInList);
        }
    }
}

上面代码是 剑指offer 中写法，剑指offer 使用C++，传递的 lastNodeInList 是一个指针，但是java中对象地址无法传递给递归调用方，所以这种方法在java中不合适

下面这个是参照网上写法

https://blog.csdn.net/Bryan__/article/details/52081877

public class Solution {
    private BinaryTreeNode head=null;
    private BinaryTreeNode tail=null;
    public BinaryTreeNode Convert(BinaryTreeNode pRootOfTree) {
        visit(pRootOfTree);
        return head;
    }
    // 中序遍历
    public void visit(BinaryTreeNode root) {
        if (root == null) {
            return;
        }
        visit(root.left);
        createList(root);
        visit(root.right);
    }
    public void createList(BinaryTreeNode cur){
        cur.left=tail;//把当前的节点接到链表的尾部
        if(tail!=null){//双向连接
            tail.right=cur;
        }else{
            head=cur;
        }
        tail=cur;//更新尾结点为当前结点，或者说：尾结点后移
    }
}

测试：

public class TestConvertBinaryTreeToList {

    BinaryTreeNode root1 = new BinaryTreeNode(10);

    @Before
    public void before() {

        BinaryTreeNode nodeA21 = new BinaryTreeNode(6);
        BinaryTreeNode nodeA22 = new BinaryTreeNode(14);
        BinaryTreeNode nodeA31 = new BinaryTreeNode(4);
        BinaryTreeNode nodeA32 = new BinaryTreeNode(8);
        BinaryTreeNode nodeA33 = new BinaryTreeNode(12);
        BinaryTreeNode nodeA34 = new BinaryTreeNode(16);

        buildTree(root1, nodeA21, nodeA22);
        buildTree(nodeA21, nodeA31, nodeA32);
        buildTree(nodeA22, nodeA33, nodeA34);
    }

    private void buildTree(BinaryTreeNode root, BinaryTreeNode left, BinaryTreeNode right) {
        root.left = left;
        root.right =right;
    }

    @Test
    public void test() {
//        BinaryTreeNode convert = ConvertBinaryTreeToLinkedList.convert(root1);
//        System.out.println(JSON.toJSONString(convert));

        Solution solution = new Solution();
        BinaryTreeNode convert = solution.Convert(root1);
        System.out.println(JSON.toJSONString(convert));
    }
}