链表中环的入口节点

题目：

如果一个链表中包含环，如何找出环的入口节点？例如，在下图所示的链表中，环的入口节点是3

分析：

​ 要解决这个问题需要分两步：

1. 如何确定链表中是否包含环？

   使用两个指针以不同的速度开始移动，如果最后两个指针能够相遇，说明链表中包含环。

2. 如何找到环的入口？

   

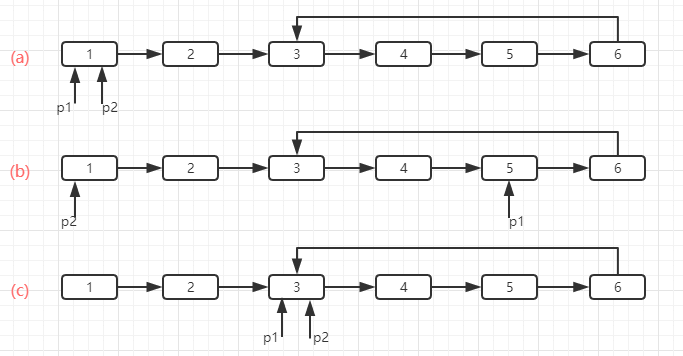
   如上图所示， p1 和 p2 初识时都指向链表的入口，然后 p1 开始移动，由于环中有4个节点，当 p1 移动 4个节点后，p2 开始移动。p1 和 p2 相遇的节点就是环的入口节点。

   如上图所示， p1 和 p2 初识时都指向链表的入口，然后 p1 开始移动，由于环中有4个节点，当 p1 移动 4个节点后，p2 开始移动。p1 和 p2 相遇的节点就是环的入口节点。

   剩余的问题就是如何获取环中节点个数？

   • 问题1 中判断是否存在环时，使用了两个速度不同的指针。如果两个指针能够相遇，说明链表中存在环，

     相遇的节点一定在环中。以这个节点为起点开始计数，当再次回到这个节点时，就可以得到环中节点的个数。

代码如下：

public class GetLoopInNodeList {

    /**
     * 获取链表中环的入口
     *
     * @param pHead 头结点
     * @return 环的入口节点
     */
    public static ListNode getLoopStart(ListNode pHead) {

        // 获取一个相遇的节点
        ListNode meetingNode = getMeetingNode(pHead);

        if (null == meetingNode) {
            return null;
        }

        // 获取环中节点个数
        int loopCount = getLoopCount(meetingNode);

        ListNode firstNode = pHead;
        ListNode secondNode = pHead;

        // firstNode 先走 loopCount 步
        for (int i = 0; i < loopCount; i++) {
            firstNode = firstNode.next;
        }
        // 等到fitstNode和secondNode相遇，相遇位置即为环的入口
        while (firstNode != secondNode) {
            firstNode = firstNode.next;
            secondNode = secondNode.next;
        }

        return firstNode;
    }

    /**
     * 获取环中节点数
     *
     * @param meetingNode 相遇节点
     * @return 环中节点数
     */
    private static int getLoopCount(ListNode meetingNode) {
        // 相遇节点存在于环中，所以初始值为1
        int loopCount = 1;
        ListNode loopNode = meetingNode;
        // 从相遇节点开始移动，到再次回到这个节点，每走一步计数加1
        while (loopNode.next != meetingNode) {
            loopCount++;
            loopNode = loopNode.next;
        }
        return loopCount;
    }

    /**
     * 获取两个速度不同的指针相遇的节点
     *
     * @param pHead 头结点
     * @return 相遇节点
     */
    private static ListNode getMeetingNode(ListNode pHead) {
        // 头结点为空，或者只有一个节点，直接返回null
        if (null == pHead || pHead.next == null) {
            return null;
        }

        // 速度较慢，每次移动1步
        ListNode slow = pHead;
        // 速度较快，每次移动2步
        ListNode fast = slow.next;

        while (fast != null && slow != null) {
            // 如果相遇，返回相遇节点
            if (fast == slow) {
                return fast;
            }
            // slow 移动1步
            slow = slow.next;
            // fast 移动1步
            fast = fast.next;
            if (fast != null) {
                // fast再移动1步
                fast = fast.next;
            }
        }
        // 最终没有相遇，说明不存在环
        return null;
    }
}

测试：

public class TestGetLoop {

    ListNode node1 = new ListNode(1);

    @Before
    public void init() {
        ListNode node2 = new ListNode(2);
        ListNode node3 = new ListNode(3);
        ListNode node4 = new ListNode(4);
        ListNode node5 = new ListNode(5);
        ListNode node6 = new ListNode(6);
        ListNode node7 = new ListNode(7);

        node1.next = node2;
        node2.next = node3;
        node3.next = node4;
        node4.next = node5;
        node5.next = node6;
        node6.next = node7;
        node7.next = node4;
    }

    @Test
    public void test() {

        ListNode loopStart = GetLoopInNodeList.getLoopStart(node1);
        System.out.println(null == loopStart ? null : loopStart.value); // 4
    }
}