从上到下打印二叉树

从上到下打印二叉树

题目一：不分行从上到下打印二叉树

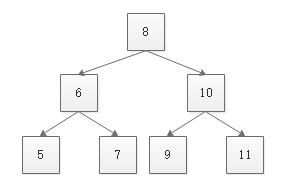
​ 从上到下打印二叉树的每个节点，同一层的节点按照从左到右的顺序打印。例如，图中二叉树，则依此打印出 {8, 6, 10, 5, 7, 9, 11} 。二叉树的节点定义如下：

public class BinaryTreeNode {

    public int value;
    public BinaryTreeNode left;
    public BinaryTreeNode right;
}

分析：

题目实际上就是二叉树的层序遍历，如上图，我们借助队列来存储节点来实现层序遍历的效果，具体操作：

1. 先将根节点入队列
2. 将根节点出队列，打印；然后将其左右子树依次入队列（若其存在）
3. 重复步骤2，直到将树遍历完为止。

上面步骤最核心的就是步骤2，步骤2为什么能够实现层序的效果呢？当该节点出栈的时候，才会将下一层的节点（其左右子树）入栈，这样就保证了一层一层的打印效果；由于左子树一直在右子树前面进行操作，所以，不会乱序，可以实现从左往右的效果。

步骤	操作	队列
1	打印节点8	节点6、节点10
2	打印节点6	节点10、节点5、节点7
3	打印节点10	节点5、节点7、节点9、节点11
4	打印节点5	节点7、节点9、节点11
5	打印节点7	节点9、节点11
6	打印节点9	节点11
7	打印节点11

代码：

public static void printNoLine(BinaryTreeNode pRoot) {
    if (null == pRoot) {
        return;
    }

    Queue<BinaryTreeNode> queue = new LinkedList<>();
    List<Integer> list = new ArrayList<>();

    // 先将根节点入队
    queue.offer(pRoot);

    // 一直遍历队列中所有元素
    while (!queue.isEmpty()) {
        // 出队
        BinaryTreeNode tempNode = queue.poll();
        list.add(tempNode.value);

        // 左子节点入队
        if (tempNode.left != null) {
            queue.offer(tempNode.left);
        }

        // 右子节点入队
        if (tempNode.right != null) {
            queue.offer(tempNode.right);
        }
    }

    System.out.println(JSON.toJSONString(list));
}

题目二：分行从上到下打印二叉树

​ 从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印一行。下图中二叉树打印结果为 右边方框中内容

分析：

​ 这道题和上面的题目类似，但是需要每层换行。所以需要两个变量，一个变量表示当前层还没有打印的节点数，另一个变量表示下一层的节点数目。

代码：

public static void printWithLine(BinaryTreeNode pRoot) {
    if (null == pRoot) {
        return;
    }

    // 本层剩余节点数
    int curRemain = 1;
    // 下一层节点数
    int nextLevel = 0;
    Queue<BinaryTreeNode> queue = new LinkedList<>();

    // 根节点入队
    queue.offer(pRoot);

    while (!queue.isEmpty()) {

        // 出队
        BinaryTreeNode tempNode = queue.poll();
        System.out.print(tempNode.value + " ");
        // 本层节点数递减
        curRemain--;

        // 左子节点入队，下一层节点数增加
        if (tempNode.left != null) {
            queue.offer(tempNode.left);
            nextLevel++;
        }

        // 右子节点入队，下一层节点数增加
        if (tempNode.right != null) {
            queue.offer(tempNode.right);
            nextLevel++;
        }

        // 如果本层节点数为0，说明已遍历完，换行，改为下层节点数
        if (curRemain == 0) {
            System.out.println();
            curRemain = nextLevel;
            nextLevel = 0;
        }
    }
}

题目三：之字形打印二叉树

​ 请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。例如，下图中的二叉树按照之字形打印结果为

分析：

​ 二叉树的根节点（节点1）打印之后，它的左子节点（节点2）和右子节点（节点3）先后保存到一个容器里面。但是打印第二层的节点时先打印节点3，再打印节点2，所以是先进后出，可以用栈类实现。

​ 接着打印第二层的两个节点。根据之字形顺序，先打印节点3，在打印节点2，并把它们的子节点保存起来。打印第三层的时候，先打印2的子节点，再打印3的子节点，所以也可以用栈来保存。

​ 依次类推，可以总结出规律，按之字形打印二叉树需要两个栈。在打印某一层节点时，把下一层子节点保存到相应的栈里。如果当前是奇数层，则先保存左子节点再保存右子节点到第一个栈里；如果当前是偶数层，则先保存右子节点再保存左子节点到第二个栈里。

​ 为什么需要两个栈？如果只有一个栈，打印根节点的时候，把 {2, 3} 保存到栈里。接下来打印节点3，把 {7, 6} 保存到栈里，这时栈里的数据为 {7, 6, 2}，接下来打印 7，无法打印2。

步骤	操作	stack1中节点	stack2中节点
1	打印节点1	2, 3
2	打印节点3	2	7, 6
3	打印节点2		7, 6, 5, 4
4	打印节点4	8, 9	7, 6, 5
5	打印节点5	8, 9, 10, 11	7, 6
6	打印节点6	8, 9, 10, 11,12 ,13	7
7	打印节点7	8, 9, 10, 11,12 ,13, 14, 15

代码：

public static void printWithZStyle(BinaryTreeNode pRoot) {
    if (null == pRoot) {
        return;
    }

    // 定义两个栈
    Stack<BinaryTreeNode> stack1 = new Stack<>();
    Stack<BinaryTreeNode> stack2 = new Stack<>();
    // 将两个栈保存到集合中
    List<Stack<BinaryTreeNode>> stackList = Arrays.asList(stack1, stack2);

    // 当前层
    int current = 0;
    // 下一层
    int next = 1;
    // 把根节点入栈（这里入的哪个栈，哪个就是第一层）
    stackList.get(current).push(pRoot);

    // 只要有一个栈有数据就继续执行
    while (!stackList.get(current).empty() || !stackList.get(next).empty()) {
        Stack<BinaryTreeNode> currentStack = stackList.get(current);
        Stack<BinaryTreeNode> nextStack = stackList.get(next);

        BinaryTreeNode tempNode = currentStack.pop();
        System.out.print(tempNode.value + " ");

        // 先进后出，
        if (current == 0) {
            if (tempNode.left != null) {
                nextStack.push(tempNode.left);
            }

            if (tempNode.right != null) {
                nextStack.push(tempNode.right);
            }
        }else{
            if (tempNode.right != null) {
                nextStack.push(tempNode.right);
            }

            if (tempNode.left != null) {
                nextStack.push(tempNode.left);
            }
        }

        // 当前栈遍历完成，交换两个栈
        if (currentStack.empty()) {
            System.out.println();
            current = 1 - current;
            next = 1- next;
        }
    }
}