重建二叉树

题目：

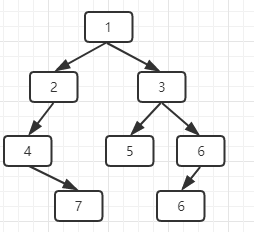
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如：前序遍历序列｛ 1, 2, 4, 7, 3, 5, 6, 8｝和中序遍历序列｛4, 7, 2, 1, 5, 3, 8，6}，重建出下图所示的二叉树并输出它的头结点。

先弄清楚几个概念：

• 前序遍历：先访问根节点，再访问左子节点，最后访问右子节点。

  上图前序遍历顺序是：10、6、4、8、14、12、16

• 中序遍历：先访问左子节点，再访问根节点，最后访问右子节点。

  上图中序遍历顺序是：4、6、8、10、12、14、16

• 后续遍历：先访问左子节点，再访问右子节点，最后访问根节点。

  上图后序遍历顺序是：4、8、16、12、16、14、10

分析：

前序遍历序列是 {1, 2, 4, 7, 3, 5, 6, 8}，中序遍历序列是 {4, 7, 2, 1, 5, 3, 8, 6}。

前序遍历第一个节点是根节点，说明1是根节点，在结合中序遍历，根节点前面是左子节点，右面是右子节点，说明 {4, 7, 2} 是左子节点，{5, 3, 8, 6} 是右子节点。

代码：

public class ReConstructBinaryTree {

    /**
     * @param preorder 前序遍历
     * @param inorder  中序遍历
     * @return
     */
    public static BinaryTreeNode construct(int[] preorder, int[] inorder) {

        if (null == preorder || null == inorder || preorder.length != inorder.length || preorder.length <= 0) {
            return null;
        }

        return construct(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
    }

    /**
     * @param preorder 前序遍历
     * @param ps       前序遍历开始位置
     * @param pe       前序遍历结束位置
     * @param inorder  中序遍历
     * @param is       中序遍历开始位置
     * @param ie       中序遍历结束位置
     * @return
     */
    private static BinaryTreeNode construct(int[] preorder, int ps, int pe, int[] inorder, int is, int ie) {
        // 开始位置大于结束位置说明已经没有需要处理的元素了
        if (ps > pe) {
            return null;
        }

        // 根节点：前序遍历的第一个节点
        int value = preorder[ps];
        // 在中序遍历的数组中找根结点的位置
        int index = 0;
        while (index <= ie && inorder[index] != value) {
            index++;
        }

        // 如果在整个中序遍历的数组中没有找到，说明输入的参数是不合法的，抛出异常
        if (index > ie) {
            throw new RuntimeException("the root node is not exist in order");
        }

        // 创建当前的根结点，并且为结点赋值
        BinaryTreeNode rootNode = new BinaryTreeNode();
        rootNode.value = value;

        // {1, 2, 4, 7, 3, 5, 6, 8}
        // {4, 7, 2, 1, 5, 3, 8, 6}
        // 递归构建当前根结点的左子树，左子树的元素个数：index-is+1 个
        // 左子树对应的前序遍历的位置在[ps+1, ps+index-is]
        // 左子树对应的中序遍历的位置在[is, index-1]
        rootNode.left = construct(preorder, ps + 1, ps + index - is, inorder, is, index - 1);
        // 递归构建当前根结点的右子树，右子树的元素个数：ie-index个
        // 右子树对应的前序遍历的位置在[ps+index-is+1, pe]
        // 右子树对应的中序遍历的位置在[index+1, ie]
        rootNode.right = construct(preorder, ps + index - is + 1, pe, inorder, index + 1, ie);

        return rootNode;
    }

    /**
     * 中序遍历二叉树
     *
     * @param rootNode 根节点
     */
    public static void printTree(BinaryTreeNode rootNode) {
        if (null != rootNode) {
            printTree(rootNode.left);
            System.out.print(rootNode.value + ", ");
            printTree(rootNode.right);
        }
    }
}

测试：

@Test
public void test() {

    int[] preorder = {1, 2, 4, 7, 3, 5, 6, 8};
    int[] inorder = {4, 7, 2, 1, 5, 3, 8, 6};

    BinaryTreeNode node = ReConstructBinaryTree.construct(preorder, inorder);
    System.out.println(node.value);
    ReConstructBinaryTree.printTree(node);
}