对称的二叉树

题目：

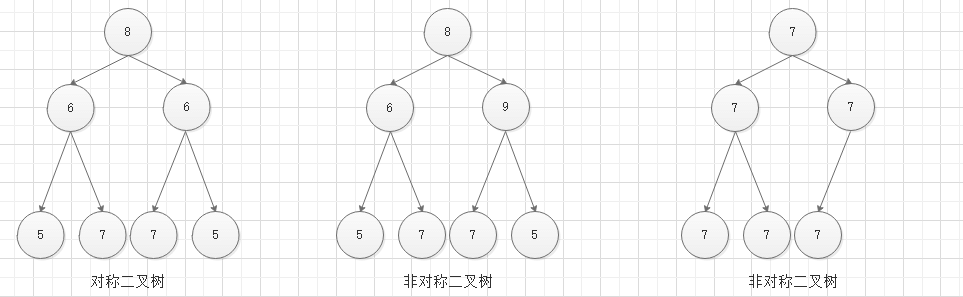
​ 请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。例如，在下图3棵二叉树中，第一棵二叉树是对称的，另外两棵不是。

分析：

​ 遍历二叉树通常有三种算法，即前序遍历、中序遍历、后序遍历。这3中算法都是先遍历左子节点再遍历右子节点。我们可否定义一种遍历算法，先遍历右子节点再遍历左子节点。比如，我们针对前序遍历定义一种对称的遍历算法，先遍历父节点，再遍历右子节点，最后遍历左子节点。

​ 如果一棵二叉树的前序遍历和它的对称遍历算法输出的序列是一致，那说明这棵二叉树是对称的。例如，第一棵二叉树，前序遍历序列为 {8, 6, 5, 7, 6, 7, 5}，对称遍历序列为 {8, 6, 5, 7, 6, 7, 5}，两个序列一样，说明它是对称的。第二棵二叉树，前序遍历序列为 {8, 6, 5, 7, 9, 7, 5}，对称遍历序列为 {8, 9, 5, 7, 6, 7, 5}，二者不一致，说明不是对称的。

​ 第三棵二叉树，前序遍历序列为 {7, 7, 7, 7, 7}，对称遍历序列为 {7, 7, 7, 7, 7}，看起来结果是一致的。但实际上它不是一棵对称二叉树。在遍历的时候需要考虑空节点。这样，它的前序遍历为 {7, 7, 7, null, null, 7, null, null, 7, 7, null, null, null}，对称遍历序列为 {7, 7, null, 7, null, null, 7, 7, null, null, 7, null, null}，二者一致。

​ 根据上述分析，可以写出如下代码

代码：

public class CheckBinaryTreeSymmetry {

    /**
     * 判断一棵二叉树是否对称
     *
     * @param pRoot 二叉树根节点
     * @return boolean
     */
    public static boolean isSymmetrical(BinaryTreeNode pRoot) {

        return isSymmetrical(pRoot, pRoot);
    }

    /**
     * 判断两棵二叉树是否对称
     *
     * @param pRoot1 二叉树1根节点
     * @param pRoot2 二叉树2根节点
     * @return
     */
    private static boolean isSymmetrical(BinaryTreeNode pRoot1, BinaryTreeNode pRoot2) {

        // 都为空，则是对称
        if (null == pRoot1 && null == pRoot2) {
            return true;
        }

        // 其中一个为空，不对称
        if (null == pRoot1 || null == pRoot2) {
            return false;
        }

        // 值不相等，不对称
        if (pRoot1.value != pRoot2.value) {
            return false;
        }

        // 两棵二叉树的左右子节点是否对称
        return isSymmetrical(pRoot1.left, pRoot2.right)
                && isSymmetrical(pRoot1.right, pRoot2.left);
    }
}

测试：

public class TestCheckSymmetry {

    BinaryTreeNode root1 = new BinaryTreeNode(8);

    @Before
    public void before() {

        BinaryTreeNode nodeA11 = new BinaryTreeNode(7);
        BinaryTreeNode nodeA12 = new BinaryTreeNode(7);
        BinaryTreeNode nodeA21 = new BinaryTreeNode(9);
        BinaryTreeNode nodeA22 = new BinaryTreeNode(2);
        BinaryTreeNode nodeA31 = new BinaryTreeNode(2);
        BinaryTreeNode nodeA32 = new BinaryTreeNode(9);

        buildTree(root1, nodeA11, nodeA12);
        buildTree(nodeA11, nodeA21, nodeA22);
        buildTree(nodeA12, nodeA31, nodeA32);

    }

    private void buildTree(BinaryTreeNode root, BinaryTreeNode left, BinaryTreeNode right) {
        root.left = left;
        root.right =right;
    }

    @Test
    public void test() {
        boolean symmetrical = CheckBinaryTreeSymmetry.isSymmetrical(root1);
        System.out.println(symmetrical);
    }
}