顺时针打印矩阵

题目：

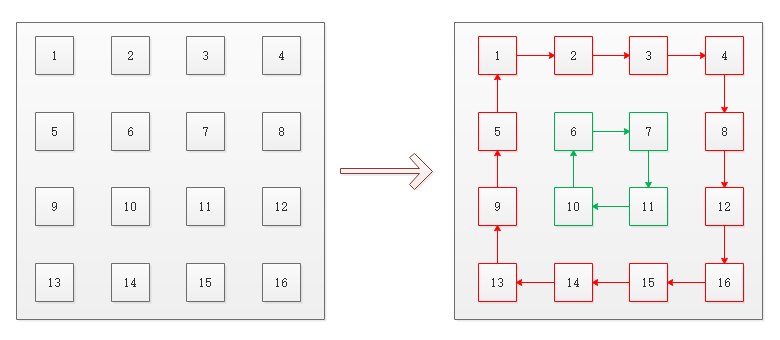
​ 输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。例如，如果输入如下矩阵：

则依次打印出数字， {1, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 10}

分析：

​ 由于是从外圈到内圈顺时针打印矩阵，我们可以把矩阵看成若干个圆，我们可以用一个循环来打印矩阵，每次打印矩阵中的一个圆。

​ 接下来分析循环结束条件，假设这个矩阵行数是 rows， 列数是 cols。打印矩阵第一圈左上角坐标是 (0, 0)，第二圈左上角坐标是 (1, 1)。依此类推，左上角的坐标中行标和列标总是相同的，于是可以选取左上角为 (start, start) 的一圈来作为分析的目标。

​ 对于一个 5x5 的矩阵，最后一圈只有一个数字，坐标为 (2, 2)，我们发现 5>2x2；对于一个 7x7 的矩阵，最后一圈只有一个数字，坐标为 (3, 3)，我们发现 7>3x2；依此类推，可以得出 循环继续的条件是 rows > start x2并且 cols > start x 2。

​ 接着分析如何打印一圈，打印一圈分四步：第一步，从左到右打印一行；第二步，从上到下打印一列；第三步，从右到左打印一行；第四步，从下到上打印一列。需要注意的是，矩阵可能只有一行或者一列，所以打印矩阵可能只需要 三步、两步或者一步。

​ 因此要判断是否需要下一步，第一步不用判断，至少都需要一步。需要第二步的条件是，至少两行，即终止行号大于起始行号；打印第三步的条件是，至少需要两列，即终止行号大于起始行号并且终止列号大于起始列号；同理，打印第四步的条件是至少需要三行两列，因此要求终止行号比起始行号至少大2，并且终止列号大于起始列号。

代码：

public class PrintMatrixSequence {

    public static void printMatrix(int[][] numbers, int rows, int cols) {

        if (null == numbers || rows <= 0 || cols <= 0) {
            return;
        }

        int start = 0;
        // 循环继续的条件
        while (rows > start * 2 && cols > start * 2) {
            printMatrixLoop(numbers, rows, cols, start);
            start++;
        }
    }

    private static void printMatrixLoop(int[][] numbers, int rows, int cols, int start) {
        // 最后一行索引
        int endRowIndex = rows - 1 - start;
        // 最后一列索引
        int endColIndex = cols - 1 - start;

        // 从左到右打印一行
        // {0, 0}、{0, 1}、{0, 2}、{0, 3}、{0, 4}
        for (int i = start; i <= endColIndex; ++i) {
            System.out.print(numbers[start][i] + ", ");
        }

        // 从上到下打印一列，需要至少两行，即结束行大于起始行
        // {0, 4}、{1, 4}、{2, 4}、{3, 4}、{4, 4}
        if (endRowIndex > start) {
            for (int i = start+1; i <= endRowIndex; ++i) {
                System.out.print(numbers[i][endColIndex] + ", ");
            }
        }

        // 从右到左打印一行，需要至少两行两列，即结束行大于起始行且结束列大于起始列
        // {4, 4}、{4, 3}、{4, 2}、{4, 1}、{4, 0}
        if (endRowIndex > start && endColIndex > start) {
            for (int i = endColIndex -1; i >= start; --i) {
                System.out.print(numbers[endRowIndex][i] + ", ");
            }
        }

        // 从下到上打印一列，需要至少三行两列，即结束列大于起始列，且结束行比起始行大2
        // {3, 0}、{2, 0}、{1, 0}
        if (endRowIndex - 1 > start && endColIndex > start) {
            for (int i = endRowIndex - 1; i >= start + 1; --i) {
                System.out.print(numbers[i][start] + ", ");
            }
        }
    }
}

测试：

public class TestPrintMatrix {

    @Test
    public void test() {

        int[][] matrix = {
            {1, 2, 3, 4, 5},
            {6, 7, 8, 9, 10},
            {11, 12, 13, 14, 15},
            {16, 17, 18, 19, 20},
            {21, 22, 23, 24, 25}
        };
        int rows = 5;
        int cols = 5;

        PrintMatrixSequence.printMatrix(matrix, rows, cols);
    }
}