平衡二叉树

题目：

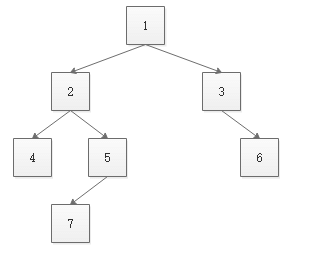
​ 输入一棵二叉树的根结点，判断该树是不是平衡二叉树。如果某二叉树中任意结点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。例如，下图中的二叉树就是一棵平衡二叉树。

分析：

1. 方法一：比较左右子树深度判断

   • 在遍历树的每个结点的时候，调用函数 getTreeDepth 得到它的左右子树的深度。
   • 如果每个结点的左右子树的深度相差都不超过1，按照定义它就是一棵平衡的二叉树。

   代码：

   public static boolean isBalance(BinaryTreeNode pRoot) {
       if (null == pRoot) {
           return true;
       }
   
       int left = DeepSolution.getTreeDepth(pRoot.left);
       int right = DeepSolution.getTreeDepth(pRoot.right);
       int diff = left - right;
       if (diff > 1 || diff < -1) {
           return false;
       }
       return isBalance(pRoot.left) && isBalance(pRoot.right);
   }
   

2. 方法二：后续遍历

   • 上面的代码固然简洁，但我们也注意到由于一个节点会重复遍历多次，这样效率就不高。
   • 如果我们用后续遍历的方式遍历二叉树，那么在遍历一个节点之前我们就已经知道了它的左、右子树。只要在遍历每个节点的时候记录它的深度（某一节点的深度等于它到叶节点路径的长度），我们就可以一边遍历一边判断每个节点是不是平衡的。

   代码：

   private static boolean isBalance(BinaryTreeNode pRoot, int depth) {
       if (pRoot == null) {
           depth = 0;
           return true;
       }
       int left = 0, right = 0;
       if (isBalance(pRoot.left, left) && isBalance(pRoot.right, right)) {
           int diff = left - right;
           if (diff <= 1 && diff >= -1) {
               depth = 1 + (left > right ? left : right);
               return true;
           }
       }
   
       return false;
   }
   
   public static boolean isBalanced(BinaryTreeNode pRoot) {
       int depth = 0;
       return isBalance(pRoot, depth);
   }
   

测试：

public static void main(String[] args) {
    BinaryTreeNode node1 = new BinaryTreeNode(1);
    BinaryTreeNode node2 = new BinaryTreeNode(2);
    BinaryTreeNode node3 = new BinaryTreeNode(3);
    BinaryTreeNode node4 = new BinaryTreeNode(4);
    BinaryTreeNode node5 = new BinaryTreeNode(5);
    BinaryTreeNode node6 = new BinaryTreeNode(6);
    BinaryTreeNode node7 = new BinaryTreeNode(7);

    node1.left = node2;
    node1.right = node3;
    node2.left = node4;
    node2.right = node5;
    node3.right = node6;
    node5.left = node7;

    System.out.println(BalanceTreeSolution.isBalance(node1));
    System.out.println(BalanceTreeSolution.isBalanced(node1));
}