智力题
1、有 25 匹⻢和 5 条赛道,赛⻢过程⽆法进⾏计时,只能知道相对快慢。问最少需要⼏场赛⻢可以知道前3名?
先把 25 匹⻢分成 5 组,进⾏ 5 场赛⻢,得到每组的排名。
再将每组的第 1 名选出,进⾏ 1 场赛⻢,按照这场的排名将 5 组先后标为 A、B、C、D、E。可以知道,A 组的第 1 名就是所有 25 匹⻢的第 1 名。⽽第 2、3 名只可能在 A 组的 2、3 名,B 组的第 1、2 名,和 C 组的第 1 名,总共 5 匹⻢。
让这 5 匹⻢再进⾏ 1 场赛⻢,前两名就是第 2、3 名。所以总共是 5+1+1=7 场赛⻢。
A 组:1,2,3,4,5 B 组:1,2,3,4,5 C 组:1,2,3,4,5 D 组:1,2,3,4,5 E 组:1,2,3,4,5
2、给定两条绳⼦,每条绳⼦烧完正好⼀个⼩时,并且绳⼦是不均匀的。问要怎么准确测量 15分钟。
- 点燃第⼀条绳⼦ R1 两头的同时,点燃第⼆条绳⼦ R2 的⼀头;
- 当 R1 烧完,正好过去 30 分钟,⽽ R2 还可以再烧 30 分钟;
- 点燃 R2 的另⼀头,15 分钟后,R2 将全部烧完。
3、有 9 个球,其中 8 个球质量相同,有 1 个球⽐较重。要求⽤ 2 次天平,找出⽐较重的那个球。
- 将这些球均分成 3 个⼀组共 3 组,选出 2 组称重,如果 1 组⽐较重,那么重球在⽐较重的那 1 组;如果 1 组重量相等,那么重球在另外 1 组。
- 对⽐较重的那 1 组的 3 个球再分成 3 组,重复上⾯的步骤。
4、有 20 瓶药丸,其中 19 瓶药丸质量相同为 1克,剩下⼀瓶药丸质量为 1.1 克。瓶⼦中有⽆数个药丸。要求⽤⼀次天平找出药丸质量 1.1克的药瓶。
- 可以从药丸的数量上来制造差异:从第 i 瓶药丸中取出 i 个药丸,然后⼀起称重。
- 可以知道,如果第 i 瓶药丸重 1.1克/粒,那么称重结果就会⽐正常情况下重 0.1 * i 克。
5、有两个杯⼦,容量分别为 5 升和 3 升,⽔的供应不断。问怎么⽤这两个杯⼦得到 4 升的⽔。
- 不能从 3 做减法得到 4,那么只能从 5 做减法得到 4,即最后⼀个运算应该为 5 - 1 = 4,此时问题转换为得到1 升的⽔;
- 1 升的⽔可以由 3 做减法得到,3 - 2 = 1,此时问题转换为得到 2 升的⽔;
- 5 - 3 = 2
6、有 100 个囚犯分别关在 100 间牢房⾥。牢房外 有⼀个空荡荡的房间,房间⾥有⼀个由开关控 制的灯泡。初始时,灯是关着的。看守每次随 便选择⼀名囚犯进⼊房间,但保证每个囚犯都 会被选中⽆穷多次。如果在某⼀时刻,有囚犯 成功断定出所有⼈都进过这个房间了,所有囚 犯都能释放。游戏开始前,所有囚犯可以聚在 ⼀起商量对策,但在此之后它们唯⼀可⽤来交 流的⼯具就只有那个灯泡。他们应该设计⼀个 怎样的协议呢?
⾸先,第⼀天出来的⼈,担当“计数者”,它把灯开起来(原来开着就 不必动了), 然后每天出来⼀个囚犯。 如果他不是“计数者”,并且没有 关过灯, 并且灯开着, 那么就把灯关了。如果他是“计数者”, 如果灯 关了, 就把他开起来(计数+1)。 当然如果灯被关了99次, 那么就 去和国王说吧。
第⼀天出来的是“计数者”, 这是⼀个必然事件, 从第⼆天开始, 我们要完成以下过程 99 次
出来⼀个新的囚犯, 然后等待“计数者”出来把灯开起来。
第⼀次出来新的囚犯的概率是: 99 / 100 --- 除去计数者, 其他任何囚犯出来都满⾜要求 , 完成这⼀步的平均时间是 100 / 99 天完成上⾯这个过程后,接着要求“计数者”出来,开灯。 这个概率是 1 / 100 , 完成这⼀步的平均时间是 100 天
第⼆次, 新囚犯出来的概率是 98 / 100, 完成这⼀步的平均时间是 100 / 98 , 计数者出来的率还是 1 / 100 , 完成这⼀步的平均时间还是 100 天
...
第99次, 新囚犯出来的概率是 1 / 100 (只有⼀个囚犯没有出来了) , 计数者出来的率还是 1 / 100
然后我们把时间加起来:
100 / 99 + 100 + 100 / 98 + 100 + ... 100 / 1 + 100
= 100 * 99 + 100 * (1 / 99 + 1 / 98 + 1 / 97 + ... + 1)
= 9900 + 100 * (1 + 1 / 2 + 1 / 3 + ... 1 / 99)
1 + 1 / 2 + 1 / 3 + ... 1 / 99 这是⼀个调和级数 ⼤概等于 ln 99 + 1 ,
所以上述值为: 10417
https://www.ocf.berkeley.edu/~wwu/papers/100prisonersLightBulb.pdf
7、家⾥有两个孩⼦,⼀个是⼥孩,另⼀个也是⼥孩的概率是多少?
https://www.bilibili.com/video/BV1ws411j77v
李永乐⽼师 yyds
ans : 1/3
8、参赛者会看⻅三扇关闭了的⻔,其中⼀扇的后 ⾯有⼀辆汽⻋,选中后⾯有⻋的那扇⻔可赢得 该汽⻋,另外两扇⻔后⾯则各藏有⼀只⼭⽺。 当参赛者选定了⼀扇⻔,但未去开启它的时 候,节⽬主持⼈开启剩下两扇⻔的其中⼀扇, 露出其中⼀只⼭⽺。主持⼈其后会问参赛者要 不要换另⼀扇仍然关上的⻔。问题是:换另⼀ 扇⻔会否增加参赛者赢得汽⻋的机率。
https://www.bilibili.com/video/av25648623/
李永乐⽼师 yyds
ans : 换, 不换1/3 ,换2/3
9、⼀副牌52张,告诉瞎⼦⾥⾯有10张牌是正⾯朝 上的, 要求瞎⼦把这52张牌分成两堆, 并且每堆 牌正⾯朝上的张数相同,可任意翻动牌,但是 ⼀直不可以看。
分成10和42, 10 中的所有牌。
proof: 第⼀堆(10张牌⾥有x张向上),全翻 = 10-x 张向上,等于第⼆堆向上的牌数
10、有⽆限的⽔,5L和6L 的桶精确装4L ⽔
通⽤解法: ⽤⼩的桶不断往⼤桶填⽔
这⾥: 5L桶 6L桶
0 0
5 0
0 5
5 5
4 6
11、1000瓶药,有⼀些可能有毒,⽤⽼⿏来喝药, 喝到有毒的⼀周就死。⼀周内⾄少需要多少只 ⽼⿏才能检测到哪些有毒
⼆进制,死=1,不死=0,⽼⿏=bit,答案 lg1000 = 10
12、25匹⻢,5个赛道,最少需要⽐赛⼏次才能知 道前3名
赛⻢经典问题: 5+1+1 = 7次
13、13个⽯头,有⼀个⽐较重其他都⼀样,⽤天平 测量最多需要⼏次才能测出重的那个
⼀般都是分成3份ABC,称A和B,如果A=B,那么在C那,A>B 在A那,A<B 在B那 .
⼀次排除了2/3.
4 4 5
- 如果 4 == 4 在 5 ⾥⾯ 分为 2 2 1
1.1) 如果 2 == 2 在 1 那 ok 两次
1.2) 如果 2 != 2 称 1 1 ,那个沉就是答案,三次 - 4 != 4 在 沉的那堆⾥⾯
2.1) 称2 2 排除 2个 再称1 1 ,那个沉就是答案,三次
ps 评论提醒,最好是1次,直接 6 6 1 ,如果平衡那个1就是答案,但是不确保能测出
14、五对夫妇举⾏家庭聚会 每⼀个⼈都可能和其他⼈握⼿, 但夫妇之间绝对不握⼿. 聚会结束时,A 先⽣提问⼤家握⼿⼏次(很关键),结果是每个⼈的握⼿次数不相同。问A先⽣的太太握⼿⼏次
⾸先有⼀个隐含的信息,他们握⼿的次数分别是0,1,2,3,4,5,6,7,8。为什么呢?显然,握⼿次数是⼩于等于8的,因为10个⼈,⾃⼰不和⾃⼰握⼿,⾃⼰不和配偶握⼿,只能是10-2=8,刚刚好⼤家的都不同所以就是0-8了
其次,握⼿x次和握⼿8-x次的是⼀家⼈。抽象来说,俩夫妻握⼿总次数刚刚好铺满其他8⼈。
⽐如0次和8次是⼀家⼈。因为⼀个⼈握了0次⼿,说明他(她)没有和其他任何⼈握⼿,⽽握了8次⼿的⼈握了别家的所有⼈的⼿,如果握了8次⼿的这个⼈和握了0次⼿的这个⼈不是⼀家⼈,握了8次⼿的这个⼈就必然握过握了0次⼿的⼈,那么,握了0次⼿的⼈就被握了8次⼿的⼈握了1次,这就⽭盾了。
再⽐如,握1次⼿的⼈和握7次⼿的⼈是⼀家⼈。因为现在⼤家都⾄少握过⼀次⼿了(和握过8次⼿的那个⼈握的),所以握过7次⼿的⼈必须和除了第⼀家和⾃⼰家的所有⼈握⼿,⽽握过1次⼿的⼈已经不能再和任何⼈握⼿了,因此,他们只能是⼀家⼈。其他同理。
接着,既然握⼿次数之和为8的必定是⼀对夫妻,九⼈中⼜没有两个⼈握⼿的次数相同,⽽0-8次握⼿⾥⾯没有配对成功的是4(成功的是0-8,1-7,2-6,3-5),所以只有A先⽣和A太太握⼿次数同为4次
15、两⼈玩游戏,在脑⻔上贴数字(正整数=1),只看⻅对⽅的,看不⻅⾃⼰的,⽽且两⼈的数字相差1。两⼈的对话: A:我不知道 B:我也不知道 A:我知道了 B:我也知道了。问A头上的字是多少,B头上的字是多少?
每⼀个数n都是 有n-1和n+1两个相邻数,但是1只有⼀个2是相邻数
A:我不知道 。不知道⾃⼰是1还是3
B:我也不知道。 如果A是1,那么B肯定是能够确定他⾃⼰是2。
A:我知道了。⾃⼰不是1 ⽽是3
B:我也知道了。 既然A知道⾃⼰,肯定是从2推出的3,那么也知道⾃⼰是2了
所以A是3,B是2
16、如果你是⼀名艾滋病患者,那么经过检测后, 结果显示为阳性的概率为 99% 。如果你并没 有携带艾滋病毒,经过检测后,结果显示为阳 性的概率仅为 1% 。也就是说,这种设备较为 ‘可靠’, 不论你是否患有艾滋病,它基本能作 出正确的判断。假如现在,⽤艾滋病检测试纸 对⾃⼰进⾏⼀次 检测,检测结果显示是阳性, 那请问你觉得⾃⼰得艾滋病的概率是多⼤?患 艾滋病的概率是 1/10000 .
当随机从总体中抽出⼀个⼈,利⽤检测试纸进⾏检测,如果检测结果呈阳性,并不意味着这个⼈⼀定患病,他患病的可能性其实不⾼,原因是没患病的⼈基数实在太⾼了。
阳性的情况(假阳+真有病): 9999/10000 * 1% + 1/10000 * 99%
真有病概率 : 1/10000 * 99% / ( 9999/10000 * 1% + 1/10000 *99% ) 约1%
后续问题: 连续2次都是阳性,真有病的概率?
阳性的情况(假阳+真有病): 9999/10000 * 1%* 1% + 1/10000 * 99% * 99%
真有病概率 : 1/10000 * 99% * 99% / ( 9999/10000 * 1% * 1% + 1/10000 * 99% * 99%) 约50%
17、烧⼀根不均匀的绳,从头烧到尾总共需要1个⼩时。现在有若⼲条材质相同的绳⼦,问如何⽤烧绳的⽅法来计时⼀个⼩时⼗五分钟呢?
1 同时两头 2 ⼀头 等1 烧完再点2的另⼀头,等2烧完再点燃3,等3 完就是1⼩时15min
18、有10瓶药,每瓶有10粒药,其中有⼀瓶是变质 的。好药每颗重1克,变质的药每颗⽐好药重 0.1克。问怎样⽤天秤称⼀次找出变质的那瓶药。
编号1-10 分别取1-10颗,重量为x, 坏药编号为 (x - 55) /0.1
19、有7克、2克砝码各⼀个,天平⼀只,如何只⽤
这些物品三次将140克的盐分成50、90克各⼀份?
第⼀步:把140克盐分成两等份,每份70克。
第⼆步:把天平⼀边放上2+7克砝码,另⼀边放盐,这样就得到9克和61克分开的盐。
第三步:将9克盐和2克砝码放在天平⼀边,另⼀边放盐,这样就得到11克和50克。于是50和90就分开了
20、有⼀辆⽕⻋以每⼩时15公⾥的速度离开洛杉矶 直奔纽约,另⼀辆⽕⻋以每⼩时20公⾥的速度 从纽约开往洛杉矶。如果有⼀只⻦,以外30公 ⾥每⼩时的速度和两辆⽕⻋现时启动,从洛杉 矶出发,碰到另⼀辆⻋后返回,依次在两辆⽕ ⻋来回的⻜⾏,直道两⾯辆⽕⻋相遇,假设洛 杉矶到纽约的距离为s, 请问,这只⼩⻦⻜⾏了 多⻓距离?
那⼩⻦⻜⾏的距离就是(s/(15+20))*30。 时间 * 速度
21、你有两个罐⼦,50个红⾊弹球,50个蓝⾊弹球,随机选出⼀个罐⼦,随机选取出⼀个弹球 放⼊罐⼦,怎么给红⾊弹球最⼤的选中机会? 在你的计划中,得到红球的准确⼏率是多少?
罐1 : 红1
罐2 : 红49+蓝50
红概率 = 1/2 * 1 + 1/2 * 49 /(49+50) 约3/4
22、想象你在镜⼦前,请问,为什么镜⼦中的影像 可以颠倒左右,却不能颠倒上下?
因为⼈的两眼在⽔平⽅向上对称。
23、病狗问题 ⼀个住宅区内有100户⼈家,每户⼈ 家养⼀条狗,每天傍晚⼤家都在同⼀个地⽅遛 狗。已知这些狗中有⼀部分病狗,由于某种原 因,狗的主⼈⽆法判断⾃⼰的狗是否是病狗, 却能够分辨其他的狗是否有病,现在,上级传 来通知,要求住户处决这些病狗,并且不允许 指认他⼈的狗是病狗(就是只能判断⾃⼰的), 过了7天之后,所有的病狗都被处决了,问, ⼀共有⼏只病狗?为什么?
https://www.bilibili.com/video/av27732823/
李永乐⽼师,yyds
24、桌上有100个苹果,你和另⼀个⼈⼀起拿,⼀ ⼈⼀次,每次拿的数量⼤于等于1⼩于等于5, 问:如何拿能保证最后⼀个苹果由你来拿?
分析:如果要保证拿最后⼀个,那么就得保证拿到第94个,以此类 推,要拿第94个,就要保证拿到第88个、82、76、70...最后只要保证 你拿到第四个就⾏了,所以看下⾯:
解答:只需要你先拿,第⼀次拿4个,以后看对⽅拿的个数,根据对 ⽅拿的个数,保证每轮对⽅和你拿的加起来是6就⾏了,其实就是保 证你拿到4,还要拿到10,16...直到94
25、两位盲⼈ , 他们都各⾃买了两对⿊袜和两对⽩ 袜,⼋对袜⼦的布质、⼤⼩完全相同,⽽每对 袜都有⼀张商标纸连着。两位盲⼈不⼩⼼将⼋ 对袜⼦混在⼀起。 他们每⼈怎样才能取回⿊袜 和⽩袜各两对呢?
每⼀对分开,⼀⼈拿⼀只,因为袜⼦不分左右脚的;
26、⼀群⼈开舞会,每⼈头上都戴着⼀顶帽⼦。帽 ⼦只有⿊⽩两种,⿊的⾄少有⼀顶。每个⼈都 能看到其它⼈帽⼦的颜⾊,却看不到⾃⼰的。 主持⼈先让⼤家看看别⼈头上戴的是什⺓帽 ⼦,然后关灯,如果有⼈认为⾃⼰戴的是⿊帽 ⼦,就打⾃⼰⼀个⽿光。第⼀次关灯,没有声 ⾳。于是再开灯,⼤家再看⼀遍,关灯时仍然 鸦雀⽆声。⼀直到第三次关灯,才有劈劈啪啪 打⽿光的声⾳响起。问有多少⼈戴着⿊帽⼦?
病狗问题
27、有三筐⽔果,⼀筐装的全是苹果,第⼆筐装的
全是橘⼦,第三筐是橘⼦与苹果混在⼀起。筐 上的标签都是错的 , 你的任务是拿出其中⼀ 筐,从⾥⾯只拿⼀只⽔果,然后正确写出三筐 ⽔果的标签。
从标着“混合”标签的筐⾥拿⼀只⽔果,就可以知道另外两筐装的是什么⽔果了。
28、⼀个⼩猴⼦边上有100 根⾹蕉,它要⾛过50 ⽶ 才能到家,每次它最多搬50 根⾹蕉,每⾛1 ⽶ 就要吃掉⼀根,请问它最多能把多少根⾹蕉搬 到家⾥。
设 ⼩猴从 0 ⾛到 50, 到 A 点时候他可以直接抱⾹蕉回家了, 可是到 A 点时候他⾄少消耗了3A 的⾹蕉( 到A, 回0, 到A), ⼀个限制就是⼩猴只 能抱 50 只⾹蕉, 那么在 A 点⼩猴最多 49 只⾹蕉.100-3A=49, 所以 A=17.
0 -> 17 放下 50 - 2*17 = 16 根
17-> 0 消耗完
0 -> 17 还有 50 - 17 + 16 = 49 根
直接回家 49 - (50 - 17) = 16 根
29、连续整数之和为1000的共有⼏组?
⾸先1000为⼀个解。连续数的平均值设为x,1000必须是x的整数倍。 假如连续数的个数为偶数个,x就不是整数了。x的2倍只能是5,25, 125才⾏。因为平均值为12.5,要连续80个达不到。125/2 = 62.5是可 以的。即62,63,61,64,等等。连续数的个数为奇数时,平均值为 整数。1000为平均值的奇数倍。1000 = 2×2×2×5×5×5;x可以为2, 4,8,40,200排除后剩下40和200是可以的。所以答案为平均值为
62.5,40,200,1000的4组整数。
leetcode 相关:
https://leetcode-cn.com/problems/consecutive-numbers-sum/
18#楼给了个好⼀些的解法,⼤家可以参考⼀下
30、据说有⼈给酒肆的⽼板娘出了⼀个难题:此⼈ 明明知道店⾥只有两个舀酒的勺⼦,分别能舀 7两和11两酒,却硬要⽼板娘卖给他2两酒。聪 明的⽼板娘毫不含糊,⽤这两个勺⼦在酒缸⾥ 舀酒,并倒来倒去,居然量出了2两酒,聪明 的你能做到吗?
7 0
0 7
7 7
3 11
3 0
0 3
7 3
0 10
7 10
6 11
6 0
0 6
7 6
2 11
31、在9个点上画10条直线,要求每条直线上⾄少有三个点?
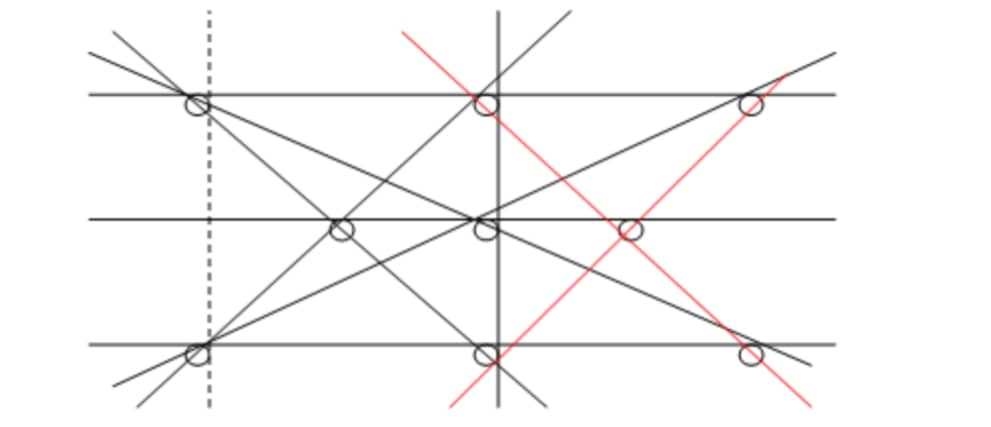
32、五个囚犯先后从100颗绿⾖中抓绿⾖。抓得最多和最少的⼈将被处死,不能交流,可以摸出剩下绿⾖的数量,谁的存活⼏率最⼤?
1、他们都是很聪明的⼈;2、他们的原则是先 求保命,再去多杀⼈;3、100颗不必都分完, 但要保证每⼈⾄少抓⼀颗;4、若有重复的情 况,则也算最⼤和最⼩,⼀并处死。
https://www.zhihu.com/question/19912025
33、有甲、⼄两⼈,其中,甲只说假话,⽽不说真 话;⼄则是只说真话,不说假话。但是,他们 两个⼈在回答别⼈的问题时,只通过点头与摇 头来表示,不讲话。有⼀天,⼀个⼈⾯对两条 路:A与B,其中⼀条路是通向京城的,⽽另⼀ 条路是通向⼀个⼩村庄的。这时,他⾯前站着 甲与⼄两⼈,但他不知道此⼈是甲还是⼄,也 不知道“点头”是表示“是”还是表示“否”。现 在,他必须问⼀个问题,才可能断定出哪条路 通向京城。那么,这个问题应该怎样问?
这个⼈只要站在A与B任何⼀条路上,然后,对着其中的⼀个⼈问: “如果我问他(甲、⼄中的另外⼀个⼈)这条路通不通向京城,他会怎 么回答?”如果甲与⼄两个⼈都摇头的话,就往这条路向前⾛去,如果 都点头,就往另⼀外⼀条⾛去。
f(g(x)) = g(f(x))
34、甲、⼄、丙三个⼈在⼀起做作业,有⼀道数学 题⽐较难,当他们三个⼈都把⾃⼰的解法说出 来以后,甲说:“我做错了。”⼄说:“甲做对 了。”丙说:“我做错了。” , 在⼀旁的丁看到他 们的答案并听了她们的意⻅后说:“你们三个 ⼈中有⼀ 个⼈做对了,有⼀个⼈说对了。”请 问,他们三⼈中到底谁做对了?
假设丙做对了,那么甲、⼄都做错了,这样,甲说的是正确的,⼄、丙都说错了,符合条件,因此,丙做对了。
35、50名运动员按顺序排成⼀排,教练下令:“单 数运动员出列!”剩下的运动 员重新排列编 号,教练⼜下令:“单数运动员出列!”如此下 去,最后只剩下⼀个⼈,他是⼏号运动员?最 后剩下的⼜是谁?
教练下令“单数”运动员出列时,教练只要下5次命令,就能知道剩下的 那个⼈。此⼈在下第五次令之前排序为2,在下4次令之前排序为4, 在下3次令之前排序为8,在下2次令之前排序为16,在下1次令之前排 序为32,即32位运动员。 因此:32号。
36、赵⼥⼠买了⼀些⽔果和⼩⻝品准备去看望⼀个 朋友,谁知,这些⽔果和⼩⻝品被他的⼉⼦们 偷吃了,但她不知道是哪个⼉⼦。为此,赵⼥ ⼠⾮常⽣⽓,就盘问4个⼉⼦谁偷吃了⽔果和 ⼩⻝品。⽼⼤说道:“是⽼⼆吃的。”⽼⼆说 道:“是⽼四偷吃的。”⽼三说道:“反正我没 有偷吃。”⽼四说道:“⽼⼆在说谎。”这4个⼉ ⼦中只有⼀个⼈说了实话,其他的3个都在撒 谎。那么,到底是谁偷吃了这些⽔果和⼩⻝ 品?
是⽼三偷吃了⽔果和⼩⻝品,只有⽼四说了实话。⽤假设法分别假设 ⽼⼤、⽼⼆、⽼三、⽼四都说了实话,看是否与题意⽭盾,就可以得 出答案
37、某企业⽼板在对其员⼯的思维能⼒进⾏测试时 出了这样⼀道题:某⼤型企业的员⼯⼈数在 1700~1800之间,这些员⼯的⼈数如果被5除 余3,如果被7除余4,如果被11除余6。那么, 这个企业到底有多少员⼯?员⼯⼩王略想了⼀ 下便说出了答案,请问他是怎么算出来的?
对题⽬中所给的条件进⾏分析,假如把全体员⼯的⼈数扩⼤2倍,则 它被5除余1,被7除余1,被11除余1,那么,余数就相同了。假设这 个企业员⼯的⼈数在3400 - 3600之间,满⾜被5除余1,被7除余1, 被11除余1的数是
( x - 1 ) % 5 ==0
( x - 1 ) % 7 ==0
( x - 1 ) % 11 ==0
lcm (5 , 7 , 11 ) = 35 * 11 = 385
385 * 9 = 3465
x = 3466,符合要求,所以这个企业共有1733个员⼯。
38、⽼师让幼⼉园的⼩朋友排成⼀⾏,然后开始发 ⽔果。⽼师分发⽔果的⽅法是这样的:从左⾯ 第⼀个⼈开始,每隔2⼈发⼀个梨;从右边第 ⼀个⼈开始,每隔4⼈发⼀个苹果。如果分发 后的结果有10个⼩朋友既得到了梨,⼜得到了 苹果,那么这个幼⼉园有多少个⼩朋友?
158个⼩朋友。
10个⼩朋友拿到梨和苹果最少⼈数是(2+1)× (4+1)×(101)+1=136⼈,然后从左右两端开始向外延伸,假设梨 和苹果都拿到的⼈为“1”,左右两边的延伸数分别为:3×5-3=12⼈, 3×5-5=10⼈。所以,总⼈数为136+12+10=158。
39、有⼀个外地⼈路过⼀个⼩镇,此时天⾊已晚, 于是他便去投宿。当他来到⼀个⼗字路⼝时, 他知道肯定有⼀条路是通向宾馆的,可是路⼝ 却没有任何标记,只有三个⼩⽊牌。第⼀个⽊ 牌上写着:这条路上有宾馆。第⼆个⽊牌上写 着:这条路上没有宾馆。第三个⽊牌上写着: 那两个⽊牌有⼀个写的是事实,另⼀个是假 的。相信我,我的话不会有错。假设你是这个 投宿的⼈,按照第三个⽊牌的话为依据,你觉 得你会找到宾馆吗?如果可以,那条路上有宾 馆哪条路上有宾馆
假设第⼀个⽊牌是正确的,那么第⼀个⼩⽊牌所在的路上就有宾馆, 第⼆条路上就没有宾馆,第⼆句话就该是真的,结果就有两句真话 了;假设第⼆句话是正确的,那么第⼀句话就是假的,第⼀⼆条路上 都没有宾馆,所以⾛第三条路,并且符合第三句所说,第⼀句是错误 的,第⼆句是正确的。
40、有⼀富翁,为了确保⾃⼰的⼈身安全,雇了双 胞胎兄弟两个作保镖。兄弟两个确实尽职尽 责,为了保证主⼈的安全,他们做出如下⾏事 准则: a.每周⼀、⼆、三,哥哥说谎; b.每逢四、五、六,弟弟说谎; c.其他时间两⼈都说真话。 ⼀天,富翁的⼀个朋友急着找富翁,他知道要 想找到富翁只能问兄弟俩,并且他也知道兄弟 俩个的做事准则,但不知道谁是哥哥,谁是弟 弟。另外,如果要知道答案,就必须知道今天 是星期⼏。于是他便问其中的⼀个⼈:昨天是 谁说谎的⽇⼦?结果两⼈都说:是我说谎的⽇ ⼦。你能猜出今天是星期⼏吗?
⾸先分析,兄弟两个必定有⼀个⼈说真话,其次,如果两个⼈都说真 话,那么今天就是星期⽇,但这是不可能的,因为如果是星期⽇,那 么两个⼈都说真话,哥哥就说谎了。 假设哥哥说了真话,那么今天⼀ 定就是星期四,因为如果是星期四以前的任⼀天,他都得在今天再撒 ⼀次谎,如果今天星期三,那么昨天就是星期⼆,他昨天确实撒谎 了,但今天也撒谎了,与假设不符,所以不可能是星期⼀、⼆、三。 由此类推,今天也不会是星期五以后的⽇⼦,也不是星期⽇。 假设弟 弟说了真话,弟弟是四五六说谎,那么先假设今天是星期⼀,昨天就 是星期⽇,他说谎,与题设⽭盾;今天星期⼆,昨天就是星期⼀,不 合题意;⽤同样的⽅法可以去掉星期三的可能性。如果今天星期四, 那么他今天就该撒谎了,他说昨天他撒谎,这是真话,符合题意。假 设今天星期五,他原本应该撒谎但他却说真话,由“昨天我撒谎了”就 知道不存在星期五、六、⽇的情况,综上所述,两个结论都是星期 四,所以今天星期四。
41、对地理⾮常感兴趣的⼏个同学聚在⼀起研究地 图。其中的⼀个同学在地图上标上了标号A、 B、C、D、E,让其他的同学说出他所标的地 ⽅都是哪些城市。甲说:B是陕⻄。E是⽢肃; ⼄说:B是湖北,D是⼭东;丙说:A是⼭东, E是吉林;丁说:C是湖北,D是吉林;戊说: B是⽢肃,C是陕⻄。这五个⼈每⼈只答对了⼀ 个省,并且每个编号只有⼀个⼈答对。你知道 ABCDE分别是哪⼏个省吗?
假设甲说的第⼀句话正确,那么B是陕⻄,戊的第⼀句话就是错误 的,戊的第⼆句话就是正确的;C是陕⻄就不符合条件。甲说的第⼆ 句话正确。那么E就是⽢肃。戊的第⼆句话就是正确的,C是陕⻄。同 理便可推出A是⼭东,B是湖北,C是陕⻄,D是吉林,E是⽢肃。
42、已知:有N架⼀样的⻜机停靠在同⼀个机场, 每架⻜机都只有⼀个油箱,每箱油可使⻜机绕 地球⻜半圈。注意:天空没有加油站,⻜机之 间只是可以相互 加油。 如果使某⼀架⻜机平 安地绕地球⻜⼀圈,并安全地回到起⻜时的机 场,问:⾄少需要出动⼏架⻜机? 注:路途中 间没有⻜机场,每架⻜机都必须安全返回起⻜ 时的机场,不许中途降落。
⼀共需要6架⻜机。假设绕地球⼀圈为1,3 架⻜机同时顺时针⻜,在 1/8 处 油量为 3/4 3/4 3/4 其中⼀辆給另外两加满往回⻜,此时油量为 1,1,到1/4 处 油量为3/4,3/4, 加满⼀辆,另⼀辆往回 2/4 ,1, 可以⻜到3/4 的位置 此时油量为0
3架⻜机往逆时针⽅向⻜,在7/8 位置3/4, 3/4, 3/4 ,⼀架给另两加 满然后往回⻜ 1,1,0,继续⻜,在3/4 位置 油量为 3/4, 3/4, 0 , 平衡⼀下 2/4 ,2/4 ,2/4 可以把之前的⻜机接回去
43、两个直径分别是2和4的圆环,如果⼩圆在⼤圆 内部绕⼤圆转⼀周,那么⼩圆⾃身转了⼏周? 如果在⼤圆的外部转,⼩圆⾃身⼜要转⼏周 呢?
⼩圆能转3周。 分析:两圆的直径分别为2、4,那么半径分别为1、 2。假如把⼤圆剪开并 拉直,那么⼩圆绕⼤圆转⼀周,就变成从直线 的⼀头移动到另⼀头。因为这条直线⻓就是⼤圆的周⻓,是⼩圆周⻓ 的2倍,所以⼩圆需要滚动2圈。 但现在⼩圆在沿⼤圆滚动的同时,⾃ 身还要作转动。⼩圆在沿着⼤圆滚动1周并回到原出发点的同时,⼩ 圆⾃身也转了1周。如果⼩圆在⼤圆的内部滚动,其⾃转的⽅向与滚 动的转向相反,因此⼩圆⾃身转了1周;如果⼩圆在⼤圆的外部滚 动,其⾃转的⽅向与滚动的转向相同,因此⼩圆⾃身转了3周。
44、在⼀个夜晚,同时有4⼈需要过⼀桥,⼀次最 多只能通过两个⼈,且只有⼀只⼿电筒,⽽且 每⼈的速度不同。A,B,C,D需要时间分别 为:1,2,5,10分钟。问:在17分钟内这四 个⼈怎么过桥?
总共是17分钟
第⼀步:A、B过花时间2分钟。
第⼆步:B回花时间2分钟。
第三步:C、D过花时间10分钟。
第四步:A回花时间1分钟。
第五步:A、B再过花时间2分钟。
整理汇总了⼀些 Java ⾯试相关的⾼质量 PDF 资料,公众号“JavaGuide”
后台回复“⾯试” 即可获取!